
Trực tâm là gì? Xác định trực tâm trong tam giác
Trực tâm của tam giác là giao điểm của 3 đường cao, nghĩa là giao điểm của các đường thẳng từ mỗi đỉnh của tam giác đến cạnh đối diện của nó tạo thành một góc vuông. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.
Trực tâm là gì?
Cụ thể: Trong hình vẽ là các đường cao, là trực tâm tam giác .
Cách xác định trực tâm của tam giác
Chú ý: a) Nếu tam giác là tam giác nhọn thì trực tâm nằm trong tam giác.

b) Nếu tam giác là tam giác vuông tại 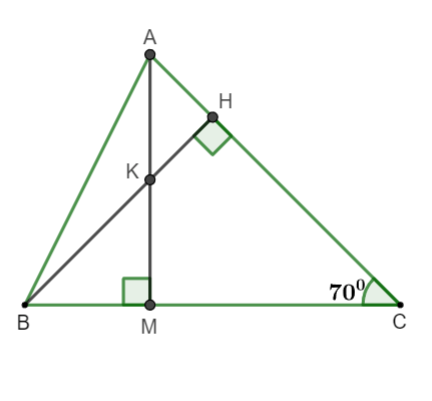 thì trực tâm trùng với điểm
thì trực tâm trùng với điểm  .
.
c) Nếu tam giác là tam giác tù thì trực tâm nằm ngoài tam giác.
Tính chất của trực tâm tam giác
Bài tập xác định, chứng minh trực tâm tam giác
Ví dụ: Cho không vuông. Gọi là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác . Từ đó hãy chỉ ra trực tâm của tam giác đó.
Hướng dẫn giải
Hình vẽ minh họa
Gọi là chân các đường vuông góc kẻ từ của ΔABC.
Xét ΔHBC có :
nên AD là đường cao từ H đến BC.
tại F nên BA là đường cao từ B đến HC
tại E nên CA là đường cao từ C đến HB.
cắt nhau tại A nên A là trực tâm của ΔHCB.
Ví dụ: Cho tam giác vuông tại có đường cao . Gọi trung điểm của là , trung điểm của là . Xác định trực tâm tam giác .
Hướng dẫn giải
Xét bài toán phụ nếu tam giác có lần lượt là trung điểm của và AC thì và .
Thật vậy, trên tia đối của tia lấy điểm sao cho
Xét tam giác AMN và tam giác CPN có
(đối đỉnh)
∆AMN = ∆ CPN (c - g - c)" width="223" height="20" data-type="0" data-latex="=> ∆AMN = ∆ CPN (c - g - c)" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20%E2%88%86AMN%20%3D%20%E2%88%86%20CPN%20(c%20%E2%80%93%20g%20%E2%80%93%20c)">
MA = CP" width="108" height="15" data-type="0" data-latex="=> MA = CP" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20MA%20%3D%20CP">, (hai cạnh và hai góc tương ứng)
Hai góc ở vị trí so le trong nên
=>(hai góc so le trong)
Xét tam giác BMC và tam giác PCM có
(cmt)
MC là cạnh chung
∆BMC = ∆PCM (c - g - c)" width="223" height="20" data-type="0" data-latex="=> ∆BMC = ∆PCM (c - g - c)" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20%E2%88%86BMC%20%3D%20%E2%88%86PCM%20(c%20%E2%80%93%20g%20%E2%80%93%20c)">
BC = NP" width="105" height="15" data-type="0" data-latex="=> BC = NP" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20BC%20%3D%20NP">, (cặp cạnh và góc tương ứng)
Hai góc ở vị trí so le trong nên
Ta lại có
BC = 2MN" width="119" height="15" data-type="0" data-latex="=> BC = 2MN" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20BC%20%3D%202MN">
Xét tam giác HAB có:
DE // AB" width="99" height="20" data-type="0" data-latex="=> DE // AB" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20DE%20%2F%2F%20AB"> (theo chứng minh bên trên)
Xét tam giác ADE có
mặt khác và
CA ⊥ DE" width="104" height="15" data-type="0" data-latex="=> CA ⊥ DE" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20CA%20%E2%8A%A5%20DE">
CA, DC" width="89" height="17" data-type="0" data-latex="=> CA, DC" class="lazy" data-src="https://tex.vdoc.vn?tex=%3D%3E%20CA%2C%20DC"> là đường cao của tam giác ADE
Mà C là giao điểm của AC và DC
=> C là trực tâm của tam giác ADE
Ví dụ: Cho cân tại A có , đường cao cắt đường trung tuyến tại . Chứng minh và tính ?
Hướng dẫn
Hình vẽ minh họa
Do cân tại A và AM là trung tuyến
⇒ AM cũng là đường cao ứng với BC
tại M.
Mặt khác và nên K là trực tâm .
Suy ra K thuộc đường cao hạ từ C của ∆ABC
Ta có:
Link nội dung: https://itt.edu.vn/truc-tam-la-giao-cua-ba-duong-gi-a17779.html